Find the number of islands

We all know that for any interview point of view the graph data structures are very much important. Because in most of the cases we end up having graph-based data structures in real-life problems. Social Graph APIs such as Facebook's Graph API, Recommendation Engines such as Yelp's GraphQL API, Path Optimization Algorithms such as Google Maps Platform (Maps, Routes APIs) and Car Navigations, Web Analytics and Scientific Computations are some of the finest use cases for Graph Data Structures.

As a result, there is a good possibility that you will be evaluated on your implementations of graphs and trees, as well as other algorithms, during an interview. As a matter of fact, it is prudent for every developer to study and apply these data structures.

As part of that, I'll try to deconstruct one of the most popular interview questions about connected graphs in the business.

So let's get this party started.....

The question is as simple as it can get.

Given a boolean 2D matrix, find the number of islands. A group of connected 1s forms an island.

So that means you are given a matrix that is 2 dimensional. Which consist of 1's and 0's where "0" is water and "1" island. there are asking you to find the number of islands in the matrix.

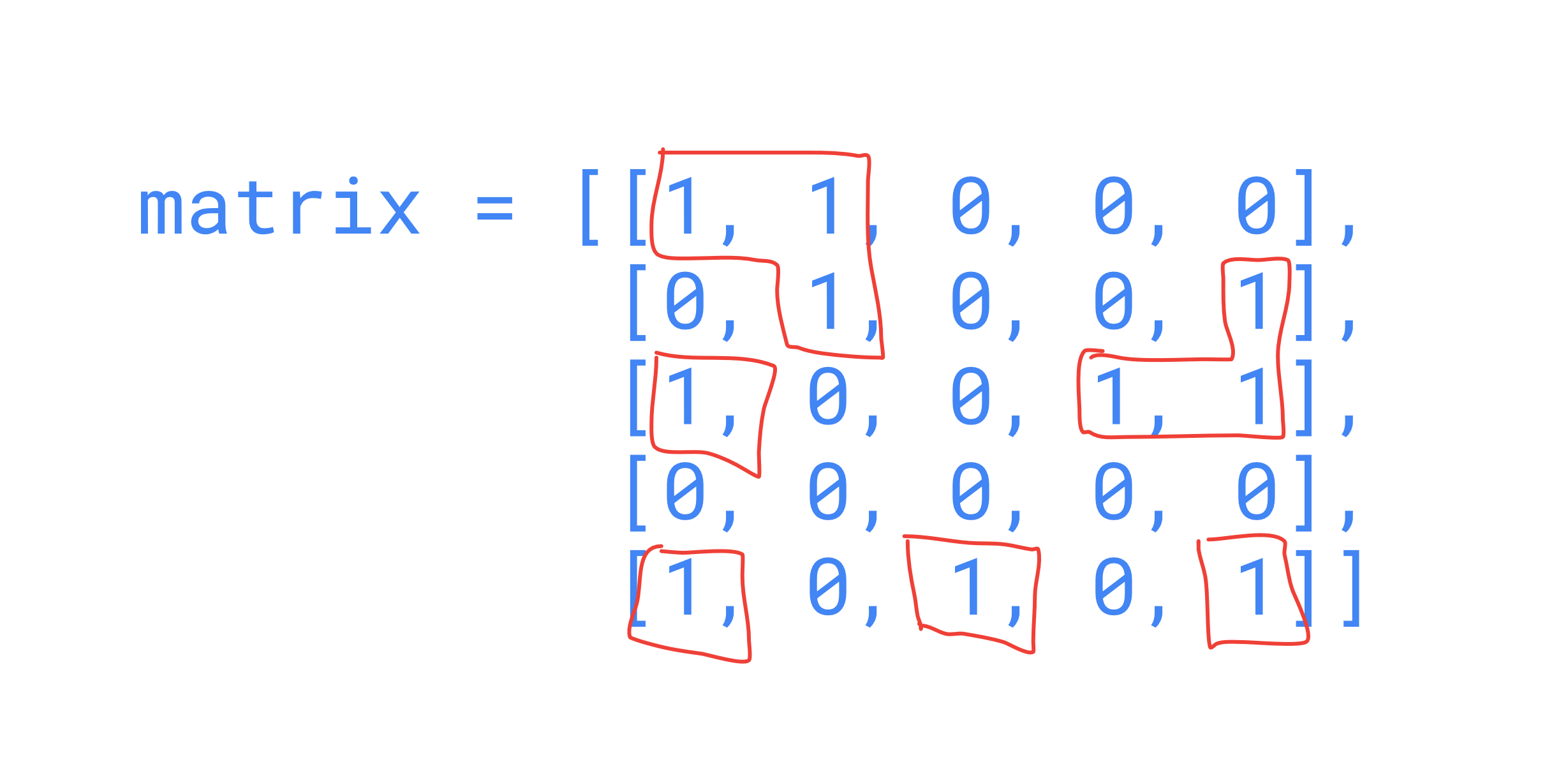
autodraw 18_10_2021.png

Note: We have only considered the 4 sides of an element for a better understanding. Rather considering the diagonals sides as well.

Ok ! Now we have understood the problem. Let's see how to solve them.

So how would you solve this problem when you see this in your own interview.

PANIC 🥲 PANIC 🤷‍♂️

If you have no idea it's ok. All you need is to understand Connected Components in a Graph. Here is a geeksforgeeks LINK for you to have a quick look at it.

Now I assume you have a better understanding of Connected Components in a Graph. One can solve this by simply using the concept of connected components and DFS. So let's get into the code and I will explain along with the code for better understanding

def islandfinder(graph: list):
    no_of_islands = 0
    for i in range(len(graph)):
        for j in range(len(graph[i])):
            if graph[i][j] == 1:
                print(str(graph) + ' ' + str(no_of_islands))
                no_of_islands += 1

                dfs(i, j, graph)
    print(no_of_islands)

To begin with, I wrote a function that says island_finder

what I intend to do is, to go to each element present in the 2D matrix and check if the element in the matrix[i][j] is "1" or "0"
If the element in the matrix[i][j] is a "1" that is water I want to find all the connected elements of that element.
To iterate through the matrix which is nothing but the list of lists in python. I have written two loops "i", "j"
And then if the condition is met I will pass the element to a dfs to find the element.

So now we will see who I managed to write the dfs for this below.

def dfs(i, j, graph):
    n = len(graph[0])
    m = len(graph)
    if i < 0 or i >= m or j < 0 or j >= n or graph[i][j] != 1:
        return
    graph[i][j] = 2

    dfs(i, j + 1, graph)
    dfs(i, j - 1, graph)
    dfs(i + 1, j, graph)
    dfs(i - 1, j, graph)

So this function dfs above does nothing but find DFS. But with a little twist. 😁

-So once the element is passed to this function that is dfs, The dfs first checks for the edge cases where the edge elements of the graphs can throw an error.

once we ignore the edge cases we mark the present element "2" we can mark with anything. This just not to resend the element to find_island function
And use a recursive function and pass the 4 sides of the given element to the same dfs function to find the connected elements.

I have written the code with the inclusion of diagonal elements and with a different example below.

matrix = [
        [1, 0, 1, 0, 0, 0, 1, 1, 1, 1],
        [0, 0, 1, 0, 1, 0, 1, 0, 0, 0],
        [1, 1, 1, 1, 0, 0, 1, 0, 0, 0],
        [1, 0, 0, 1, 0, 1, 0, 0, 0, 0],
        [1, 1, 1, 1, 0, 0, 0, 1, 1, 1],
        [0, 1, 0, 1, 0, 0, 1, 1, 1, 1],
        [0, 0, 0, 0, 0, 1, 1, 1, 0, 0],
        [0, 0, 0, 1, 0, 0, 1, 1, 1, 0],
        [1, 0, 1, 0, 1, 0, 0, 1, 0, 0],
        [1, 1, 1, 1, 0, 0, 0, 1, 1, 1]
    ]


def island_finder(graph: list):
    no_of_islands = 0
    for i in range(len(graph)):
        for j in range(len(graph[i])):
            if graph[i][j] == 1:
                print(str(graph) + ' ' + str(no_of_islands))
                no_of_islands += 1

                dfs(i, j, graph)
    print(no_of_islands)


def dfs(i, j, graph):
    n = len(graph[0])
    m = len(graph)
    if i < 0 or i >= m or j < 0 or j >= n or graph[i][j] != 1:
        return
    graph[i][j] = 2

    dfs(i, j + 1, graph)
    dfs(i, j - 1, graph)
    dfs(i + 1, j, graph)
    dfs(i - 1, j, graph)
    dfs(i - 1, j - 1, graph)
    dfs(i + 1, j + 1, graph)
    dfs(i + 1, j - 1, graph)
    dfs(i - 1, j + 1, graph)


island_finder(matrix)

That's it. Now pass the matrix to the find_island function and enjoy the result. 😁😎

Happy coding guys. see you next time with some more interesting problems. Till then NAMSTEY 👏👏🙌🙏

How to find the number of islands in a matrix

Comments

More from this blog

Dutch National Flag problem

How to enable Multi-Factor Authentication (MFA) for S3 buckets?

How to Deploy the static website to S3 using GitHub actions.

How to find the length of the longest substring in it with no more than K distinct characters ?

Command Palette

Comments

More from this blog